Design of Un-restrained Steel Beam (I-Section) – Worked Example

This article presents a practical worked example on the design of unrestrained steel beam (I-section) to Eurocode 3

The beam to be designed has been analysed using Etabs software as part of a frame in the article, ”Analysis of Steel Frames Allowing for Imperfections”, the resulting bending moment and shear force diagram are shown below.

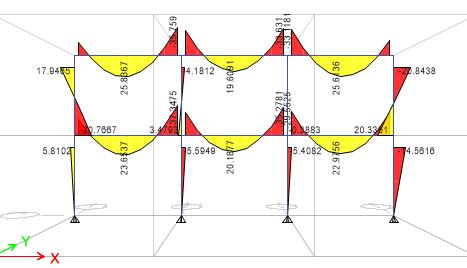
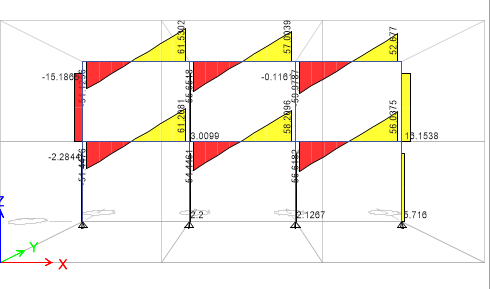
Internal forces

From the analysis results, the maximum of the internal forces acting on each beam shall be considered to be acting on the beam to be designed.

Maximum Shear Force = 61.53KN (left topmost beam)

Maximum Moment = 37.347KNm (left lower beam)

Beam Properties 

Beam section: 457 x 152 x 52 UKB S275

The properties of the steel section listed below are excerpted from SCI P363

h = 449.8mm, b = 152.4mm, t_w= 7.6mm, t_f = 10.9mm, r = 10.2mm, d = 407.6mm, i_y = 17.9cm, i_z = 3.11cm, W_ply = 1100cm³, W_plz = 133cm³, A = 66.6cm², E = 210 x 10³cm³, I_y =21400cm⁴, I_z = 645cm⁴, I_w= 0.311dm⁶, I_t = 21.4cm³

c_f/t_f = 5.71

c_w/t_w = 53.6

Cross-section Classification

We shall classify the cross-section of the beam (you should click here to study a detailed article on cross-section classification of steel cross-sections).

Influence of material strength

The UK National Annex recommends that EN 10025-2:2004 replaces Table 3 of EN 1993-1-1:2005 to determine the yield strength (fy) and ultimate strength (fu) of steel sections

Hence, for thickness of 10.9mm for grade S275 |f_y = 275MPa, f_u = 430MPa (Table 7, EN 10025-2)

$$
\varepsilon \,\,=\,\,\sqrt{\frac{235}{275}}\,\,=\,\,0.925
$$

Flanges (Outstand Element)

Since the neutral axis of the section is assumed to be within the web, the flange is in pure compression.

(Using Table 5.2 (Sheet 2 of 3) of EN 1993-1-1-2005)

c_f/t_f = 5.71mm

from the table, limiting value for class 1 is 9 ℇ = 9 x 0.925 = 8.325

since 5.71 < 8.325, the flanges are class 1

Web (Internal Element)

(Using Table 5.2 (Sheet 1 of 3) of EN 1993-1-1-2005)

c_w/t_w= 53.6

from the table, limiting value for class 1 is 72ℇ = 72 x 0.925 = 66.6

since 53.6 < 66.6, the web is class 1

The entire cross-section is class 1 in bending.

Cross-section Resistance

The column cross-section shall be verified for resistance to Shear and bending.

Shear Resistance

The expression below has to be satisfied for the section to be adequate in shear

$$
\,\,\frac{V_{Ed}}{V_{cRd}}\,\,\leqslant \,\,1
$$

$
\,\,V_{c,Rd}\,\,=\,\,V_{pl,Rd}\,\,=\,\,\frac{A_v\,\,f_y/\sqrt{3}}{\gamma _{m0}}
$

For rolled I and H sections: A_v  = A – 2bt_f  + (t_w  + 2r)t_f  ≥ ηh_wt_w

A_v  = 66.6 x 10²  – 2 + (7.6+ 2 x 10.2) x 10.9 ≥ η(449 – 2 x 10.9)7.6

A_v = 3642.88 ≥ 3252.8

A_v = 3642.88

Check 

61.52/57.38 = 0.106

Since 0.106 ≤ 1 the section is adequate in shear

Bending Resistance

For adequate moment resistance, the equation below should be satisfied.

$
\,\,\frac{M_{Ed}}{M_{cRd}}\,\,\leqslant \,\,1
$

$
\,\,Mc,Rd\,\,=\,\,Mpl,Rd\,\,=\,\,\frac{W_{ply}.\,\,f_y\,\,}{\varUpsilon _{m0}}\,\,\,\,
$  (for class 1, and class 2 sections)

$
\,\,Mc,Rd\,\,=\,\,\frac{1100 x 10^3 .\,\,275\,\,}{1 x 10^6}\,\,\,\,
$  = 302.5KNm

Check

37.347/302.5  = 0.12

Since 0.12 ≤ 1, the section is adequate in bending

Combined Shear and Bending Resistance

The maximum bending moment and shear force acts occur at the end of each beam, hence the maximum shear force shall be adopted as coincidence shear.

We shall check whether reduction in bending resistance is necessary due to the shear force.

0.5 V_pl,Rd = 0.5 x 578.38 = 289.19KN

Since V_Ed  ≤ 0.5V_{pl,Rd ,} then reduction in bending resistance is unnecessary

The section is adequate for combined bending and shear.

Stability Check

If the beam were restrained, we would have rounded off the design after verifying the combined shear and bending resistance, however the beam is un-restrained hence we have to verify its stability against lateral torsional buckling

Verify the Resistance of the Beam to Lateral torsional buckling

Lateral torsional buckling is evaluated using the expression below:

$$
M_{b,Rd}\,\,=\,\,\chi _{LT}\,\,\frac{W_y\,\,.\,\,f_y}{\varUpsilon _m}
$$

Where,

$
\,\,\chi _{LT}\,\,=\,\,\frac{1}{\phi _{LT}\,\,+\,\,\sqrt{\phi _{LT}^2\,\,+\,\,\ βλ _{LT}^2}}
$

Φ_LT = 0.5 (1 + ∝_LT( λ_LT – λ_LT,0) + βλ_LT ²)

$
\,\lambda _{LT}\,\,=\,\,\sqrt{\frac{W_y\,\,.\,\,f_y}{M_{cr}}}
$

Calculate the Elastic Critical Moment

$M_{C r}=C_1 \frac{\pi^2 E I_z}{L^2} \sqrt{\frac{I_w}{I_z}+\frac{L^2 G I_t}{\pi^2 E I_z}}$

C₁= 2.578 (This is the value of C₁ for transverse loaded member with the shape of bending moment as shown above. Click here to study in detail the theory and fundamental concept of lateral torsional buckling)

G = 80770 N/mm²

E = 21000

I_w = 0.311dm⁶, It = 21.4cm³

I_z = 645cm⁴

L = 4000mm

$M_{C r}= 1.77 \frac{3.142^2 x 210000 x 645 x 10^4} {4000^2 x 10^3} \sqrt{\frac{0.311 x 10^12}{645 x 10^4}+\frac{4000^2 x 81000 x 21.4}{3.142^2 x 210000 x 645}}$

M_cr= 565.779

Calculate the Non-dimension Slenderness

$
\,\lambda _{LT}\,\,=\,\,\sqrt{\frac{1100 x 10^3\,\,.\,\,275}{565.779 x 10^6}}
$ = 0.731

h/b = 2.95, use buckling curve c (Table 6.5, EN 1993-1-1)

∝_LT = 0.49 (using Table 6.5)

β = 0.75

λ_LT,0 = 0.4

Φ_LT  = 0.5 (1 + 0.49(0.731– 0.4) + 0.75 x 0.731²) = 0.782

Calculate the reduction factor

$
\,\,\chi _{LT}\,\,=\,\,\frac{1}{0.782\,\,+\,\,\sqrt{0.782^2\,\,+\,\,\ 0.75 x 0.731^2}}
$ = 0.807

M_b,Rd = 0.807 x 302.5 = 243.98KNm

Since 0.153 ≤ 1, the section is adequate

Check

$
\,\,\frac{M_{Ed}}{M_{bRd}}
$ = $
\,\,\frac{37.347}{243.98}
$ = 0.153

Since 0.153 ≤ 1, the section is adequate

Deflection Check

Maximum deflection for fixed beam = $
\,\,\frac{FL^4}{384EI}
$ =

F = live load = 30KN/m, L = 4000mm

Maximum deflection = $
\,\,\frac{30 x 10^3 x 4^4}{384 x 210 x 10^9 x 21400 x 10^-8}
$ x 10³ = 0.445

Limiting for beams = span/200 = 4000/200 = 20mm (Table NA.2, UK NA EN 1993-1-1)

Since 0.445 ≤ 20, then deflection criterium is satisfied.