Design of Column to Eurocode 2 using Design Chart – worked example

Column design charts are created to simplify the design of reinforced concrete columns. These charts are suitable for columns with symmetrical arrangement of reinforcement and they are produced peculiarly for columns with certain d/h or d’/h ratios.

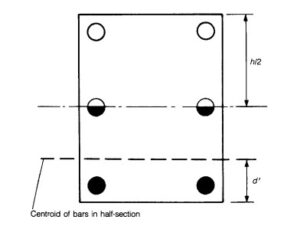
Fundamentally, columns appropriate to be designed using the charts as aides are assumed to have reinforcements concentrated at the corners of such columns, but when they are not a conservative approach should be taken such that d’ becomes the distance from the centroid of bars in half-section of the column as shown in the diagram below.

 

Although these are very essential charts for the design of symmetrically reinforced column, they however are not particularly present in Eurocode 2. They can only be found in reference materials and manuals such as “How to design concrete structures using Eurocode 2”, “Concise Eurocode” etc.

This article presents a worked example on how to design a column using these charts. The column that shall be designed is column EF which has been previously analyzed here as part of a frame using moment distribution method. The moment in the column has been obtained already and it has been evaluated to be 11.2KNm. We are left with evaluating the axial load on the column.

The axial force of a column in a structural frame may be calculated on the assumption that beams and slabs transmitting force into the particular column are simply supported. By this, the reaction from the column can be calculated which in turn serves as the load on the column. The reaction on the column shall be calculated as follows:

 

We shall first provide the frame structure below for easy reference.

From basic load distribution technique, column EF supports half of the load acting on both Beam BE and EH. Since the load acting on Beam BE and EH are 207.5 and 117.6 respectively, then the column reaction is:

207.5/2 + 117.6/2 = 162.55KN

Having calculated the axial load on the column, we can now proceed to write down the loads and other design parameters necessary for the column design.

Moment on the column (M) = 11.2KNm

Axial load on the column (N) = 162.55 KN

Length = 4m

b = 300mm

h = 350mm

fck = 25N/mm2

cover = 25mm

 

Steps in designing the column

1.  Check the Slenderness of the column.

The slenderness ratio of the column shall be compared against the limiting slenderness, if the slenderness ratio is greater than the limiting slenderness then the column is declared “slender”. The column is declared “non-slender” if otherwise. This is shown in the below steps.

a.  Calculate the effective length of the column

Since the column is braced, the Effective length (lo) is calculated thus:

$
_{\,\,l_0=0.5l\sqrt{\left( \text{1}+\,\,\frac{K_1}{\text{0.45}+\,\,K_1} \right) \left( \text{1}+\,\,\frac{K_2}{\text{0.45}+\,\,K_2} \right)}}
$

K1 and K2 are the relative flexibilities of the top and bottom ends respectively

K1 =    $
\frac{\frac{\varSigma I_c}{l}}{\frac{\varSigma 2EI_b}{l}}
$

$
\frac{\frac{\frac{bh^3}{12}}{l}}{2X\frac{\frac{bh^3}{12}}{l}\,\,+\,\,2X\frac{\frac{bh^3}{12}}{l}}
$

$
\frac{\frac{\frac{300 X 350^3}{12}}{4000}}{2X\frac{\frac{300 X 600^3}{12}}{6000}\,\,+\,\,2X\frac{\frac{300 X 600^3}{12}}{6000}}
$

= 267968.75/(1800000 + 1800000)

= 0.074

We do the same thing all over again to get K2

K2 =    $
\frac{\frac{\varSigma I_c}{l}}{\frac{\varSigma 2EI_b}{l}}
$

$
\frac{\frac{\frac{bh^3}{12}}{l}}{2X\frac{\frac{bh^3}{12}}{l}\,\,+\,\,2X\frac{\frac{bh^3}{12}}{l}}
$

$
\frac{\frac{\frac{300 X 350^3}{12}}{4000}}{2X\frac{\frac{300 X 600^3}{12}}{6000}\,\,+\,\,2X\frac{\frac{300 X 600^3}{12}}{6000}}
$

= 267968.75/(1800000 + 1800000)

= 0.074

$
_{\,\,l_0=0.5l\sqrt{\left( \text{1}+\,\,\frac{0.074}{\text{0.45}+\,\,0.074} \right) \left( \text{1}+\,\,\frac{0.074}{\text{0.45}+\,\,0.04} \right)}}
$

=2283.8699mm

b.  Calculate the radius of gyration

$
r\,\,=\,\,\sqrt{\frac{I}{A}}\,\,=\,\,\sqrt{\frac{\frac{bh^3}{12}}{b\,\,X\,\,h}}\,\,=\,\,\sqrt{\frac{\frac{\text{300}X\,\,350^3}{12}}{\text{300}X\,\,350}}\,\,\,\,=\,\,101.04
$

c.  Calculate the slenderness ratio of the column

λ =    lo/r       = 2283.8699/101.04      =     22.604

 

d. Calculate the limiting slenderness

λ_lim = (20 X A X B X C/√n)

A = 0.7, B = 1.1, C = 0.7

(All these assumptions are based on alternative suggestion by the code, check clause 5:8:3:1)

n = N_Ed /A_cf_{cd  =    n = 162.55 X 10^3 / (300 X 350 X 0.85 X 25/1.5) = 0.1}

λ_lim = (20 X 0.7 X 1.1 X 0.7/√0.1)    = 79.2

Since λ_lim (79.2) is greater than ⅄ (22.604) then the column is non-slender and second-order moment is not required.

• Compute the design moment (M_ED)

The design moment is the greatest of: max (M2, M1) + (Ned) x e

where:   M2 and M1 are the top end and bottom end moments of the column.

e is the greater between the eccentricities due to imperfection and minimum required eccentricity of a                          column.

eccentricity due to imperfection = lo/400 = 2283.8699/400   =  5.7mm

minimum eccentricity required = h/30 ≥ 20mm = 350/30 = 11.7mm

since h/30 < 20, then minimum eccentricity = 20mm

And since minimum eccentricity (20mm) is grater than that due to imperfections (5.7mm) then e is taken as the minimum eccentricity which is 20mm.

M1 = 0, M2 = 11.2KNM. so:

M_ED= M2 +N_ED X e 

M_ED = 11.2 + 162.55 X 0.02 

            = 14.451KNm

 

• Use the design Chart to determine the area of reinforcement required

        In order to use the design chart, few parameters have to be calculated

1. Determine N_ED/bhfck

  N_ED/bhfck = 162.55 X 10^3 /300 X 350 X 25   = 0.06

 

      2.  Determine M_ED/bh²fck

 M_ED/bh²fck =    14.451 X 10^6/300 X 350^2 X 25   = 0.02

 

      3.       Calculate d’/h

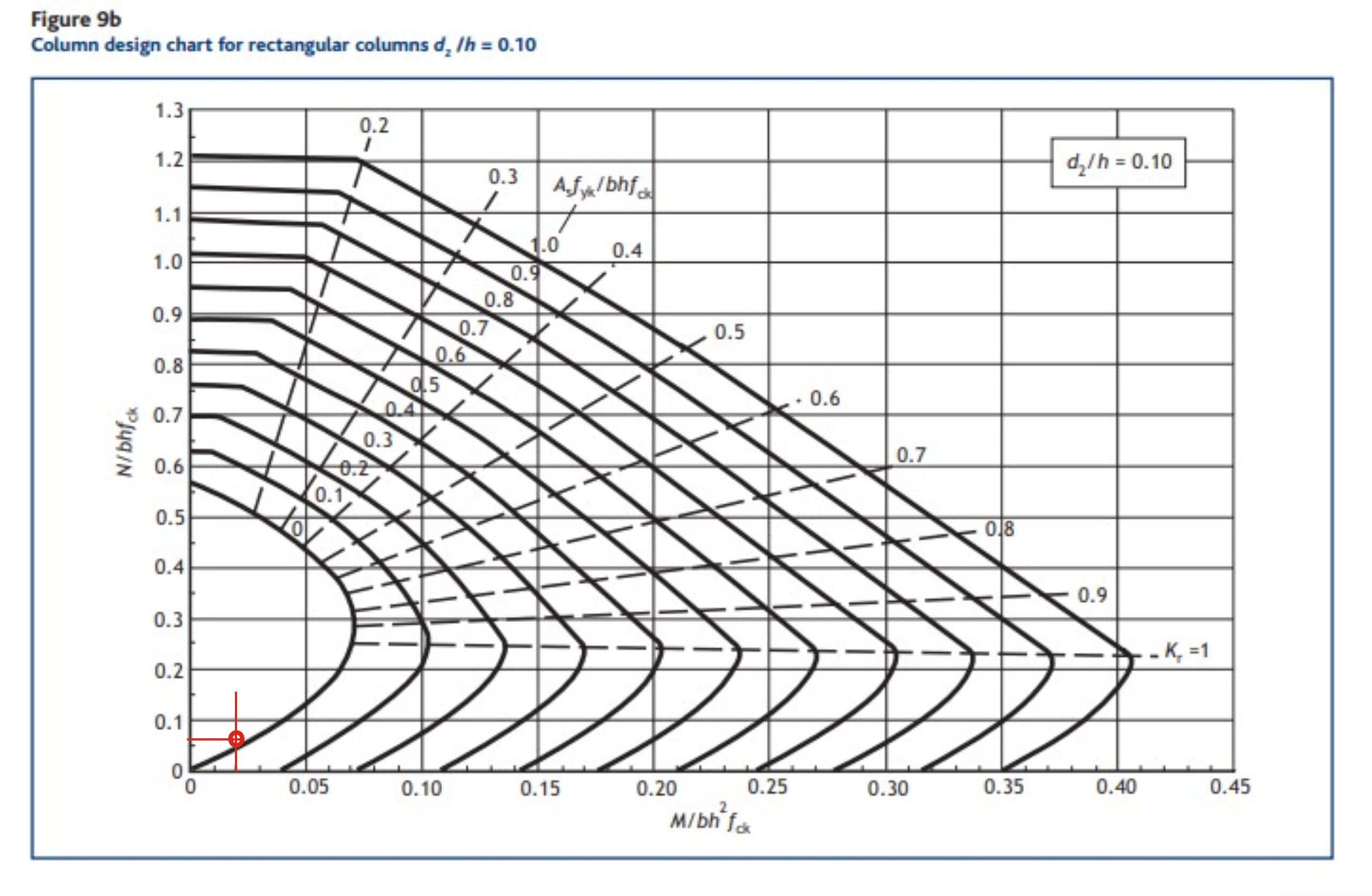
d’/h determines the exact graph that shall be used to determine the reinforcement area.

d’ = c + d/2 = 25 + 16/2 = 33

            d’/h   = 33/350 = 0.09

This is approximated to 0.1 and the design chart peculiar to d’/h = 0.1 is used. Fig 9b of “How to design concrete Structures to Eurocode 2” matches this. The chart is reproduced below.

 

From the design chart, the intersection of M_ED/bh²fck = 0.02 and N/bhfck = 0.06 falls below the 0 mark. This is shown by the red lines drawn on the chart at the almost bottom left corner.

This implies there is no need to provide reinforcement for the column. However to keep to EC2 directives minimum area of reinforcement shall be provided.

Asmin = 0.1N_ED/fyd ≥ 0.002Ac    = 37.4 

0.002Ac = 0.002 X 300 X 350 = 210

Since 0.002Ac (210) > 0.1N_ED/fyd (37.4), adopt the Area of reinforcement for the column as 210mm²

Hence provide 4Y12 (449.856mm2) as the longitudinal reinforcement of the column

 

• Determine the link diameter and spacing

 

    a.      Link diameter

 

The link diameter is the greater of;

 

• ¼ x maximum diameter of longitudinal bar
• 6mm

 

¼ x maximum diameter of longitudinal bar = ¼ x 12 = 3mm

Since 3mm > 6mm, hence use 6mm as the link diameter.

b.      Link Spacing

The link spacing should be the lesser than;

 

• 20 x minimum diameter of longitudinal bar
• lesser of the column dimension
• 400mm

20 x minimum diameter of longitudinal bar = 20 x 12 = 240mm

The lesser of the column dimension = 300m

Since 240mm is lesser than 300mm and 400mm, 240mm governs the spacing

 Provide 6mm links at 200mm spacing.