A slender column is a column that is vulnerable to buckling which affects its maximum load bearing capacity. Several codes of practice have devised diverse methods to analyse this type of column with focus on stimulating its inherent instability, this enables the column to be designed and sized appropriately for the most onerous case of load which it is likely to be subjected in its service life. BS 8110 achieves this by augmenting the moments from the general first-order analysis with additional moment (M_add); this combination of moments together with the axial load gives the most unfavorable load regime that can pratically act on the column.

 

Worked Example

The column that shall be designed is column BD that has already been analysed for moment as part of a frame here. Since the column has already been evaluated to be subjected to a moment of 42.302KNm, we are left to evaluate the axial force acting on the column.

According to clause 3.8.2.3 of BS 8110, the axial force of a column in a structural frame may be calculated on the assumption that beams and slabs transmitting force into the particular column are simply supported. By this, the reaction from the column can be calculated which in turn serves as the load on the column. The axial force on the column BD is calculated below.

 

Computation of Axial load

            For easy reference for axial load computation, the analyzed frame is reproduced below:

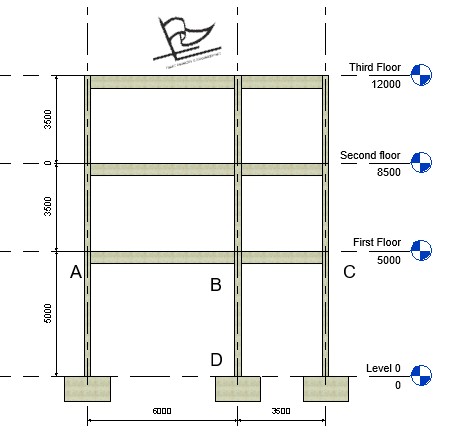
Third Floor Load take down

Characteristic permanent load on beam (gk) = 23KN/m

Characteristic variable load on beam (qk) = 36KN/m

Maximum ultimate Load acting on beam = 1.4(23) + 1.6(36) = 89.8KN/m

 

Load from third floor to column BD = (6/2 + 3.5/2) X 89.8 = 426.55

 

Second Floor and first floor Load take down

Characteristic permanent load on beam (gk) = 100KN/m

Characteristic variable load on beam (qk) = 40KN/m

Maximum ultimate Load acting on beam = 1.4(40) + 1.6(100) = 216KN/m

Load from second floor to column BD = (6/2 + 3.5/2) X 216 = 1026KN

Load from first floor to column BD = (6/2 + 3.5/2) X 216 = 1026KN

It should be noted that since we are computing for the axial load in this article, the maximum ultimate load is used all through as this gives the unfavorable axial load possible.

Axial Load on Column BD

The total axial load on the column is the summation of axial load from third, second, and first floors. This is done below:

Total Axial load on column BD = 426.55 + 1026 + 1026 = 2478.55KN

 

Steps in designing the column

Having calculated the axial load on the column, we can now proceed with the design of the column. However, before embarking on the proper design, let us write down the loads and other design parameters necessary for the column design.

Moment on the column (M) = 42.302KNm

Axial load on the column (N) = 2478.55KN

Length (l) = 5m

Breadth (b) = 250mm

Height (h) = 250mm

fck = 25N/mm2

cover = 25mm

 

• Check the Slenderness of the column.

The slenderness ratio of the column shall be compared against the limiting slenderness, if the slenderness ratio is greater than the limiting slenderness then the column is declared “slender”. The column is declared “short” if otherwise. This is shown in the below steps

 

1. Calculate the effective height of the column

Since the column is braced, the Effective height (lo) is calculated thus:

le = β lo

a)     Calculate the clear height (lo) of the column

In this example, we shall maintain the clear height to be the apparent height of the column which is 5m

b)     Evaluate the relative stiffness at the column ends

β is a coefficient dependent on the end condition of the column. Its value can be obtained from table 3.19 and 3.20 of BS 8110-1:1997, however a rigorous approach will be adopted here according to clause 2.5 of BS 8110-2: 1985.

According to BS 8110 part 2, for braced column B is adopted as the lesser of:

β = 0.7 + 0.05(αc1 + αc2)

β = 0.85 + 0.05αcmin

αc2 and αc1 are the relative flexibilities of the top and bottom ends respectively

αc2 =    $
\frac{\frac{\varSigma I_c}{l}}{\frac{\varSigma EI_b}{l}}
$

$
\frac{\frac{\frac{bh^3}{12}}{l}}{\frac{\frac{bh^3}{12}}{l}\,\,+\,\,\frac{\frac{bh^3}{12}}{l}}
$

$
\frac{\frac{\frac{250 X 250^3}{12}}{5000}}{\frac{\frac{225 X 500^3}{12}}{6000}\,\,+\,\,\frac{\frac{225 X 500^3}{12}}{3500}}
$

= 65104.2/(390625+ 669642.8)

= 0.06

We calculate for αc1

From clause 2.5.4 of BS 8110 part 2, the relative stiffness of a base designed to resist column moment is 1.0. This description above fits connection between the bottom end of the column and its base. Hence αc1 = 1.0

 

β = 0.7 + 0.05(1.0 + 0.06) =  0.753

β = 0.85 + 0.05 x 1.0 = 0.853

Since 0.753 is lesser than 0.853, hence  β = 0.753

 

c.   Determine the effective height

              l = β lo

 l = 0.753 x 5000 =  3765.53mm

 

2. Compare the slenderness ratio against the limiting slenderness.

lex/h and ley/b < 15 – braced column

lex/h = 3765.53/250 = 15.06

ley/b = 3765.53/250 = 15.06

Since lex/h and ley/b are not less than 15 then the column is slender and additional moment due to slenderness is required.

 

Check that the slenderness is within the slenderness limit.

 The slenderness limit is that:

Lo ≤ 60b or 100b²/h, whichever is less

5000 ≤ 60 x 250

5000 ≤ 15000

Since lo is less 60b then the slenderness limit is satisfied

 

Calculate the additional moment (M_add) due to slenderness effect

 Since the column is slender, additional moment due to slenderness is necessary.

Additional moment (M_add) = N X a_u

Calculate deflection due to slenderness

 a_u= B_a KH   

B_a = 1/2000 x (le/b)²

= 1/2000 x (3765.53/250)²  = 0.113

K can be conservatively taken to be 1 (see clause 3.8.3.1 of the code)

 

a_u    = 0.113 x 1 x 250 = 28.356

M_add = N X a_u

= 2478.55 x 28.356/1000 = 70.28KNm

 

.  Compute the design moment (M)

The design moment is the greatest of:

1.  M₂

2.  Mi+ M_add

      3.  M_1.+ M_add/2

We have excluded moment due to minimum eccentricity as this cannot be critical in a slender column. At least, the deflection due to slenderness is expected to be higher than the minimum eccentricity.

where:  M_i = 0.4 M02 + 0.6 M01 = 25.38KNm

 

M₂ = 42.302KN

M_i + M_add  = 25.38 + 70.28 = 95.66KNm

M₁ + M_add/2 = 0 + 70.28/2 = 35.14KNm

The design moment is 95.66KNm

 

Use the design Chart to determine the area of longitudinal reinforcement required

In order to use the design chart, few parameters have to be calculated

a.    Determine N/bh

N/bh = 2478.55 x 10^3 /250 X 250   = 39.65

 

b.     Determine M/bh²

M/bh² =    95.66 X 10^6/250 X 250²   = 6.1

 

c.    Calculate d/h

d/h determines the exact graph that shall be used to determine the reinforcement area.

d = h- c + ϕ/2 + ϕ

= 250 – 25 – 16/2 – 10 = 207mm

d/h   = 207/250 = 0.8

The design chart with parameters which conforms with d/h = 0.9, fcu = 25N/mm2, and fy = 460N/mm2 is used. Chart No 22 in BS 8110 Part 3 matches this. The chart is reproduced below.

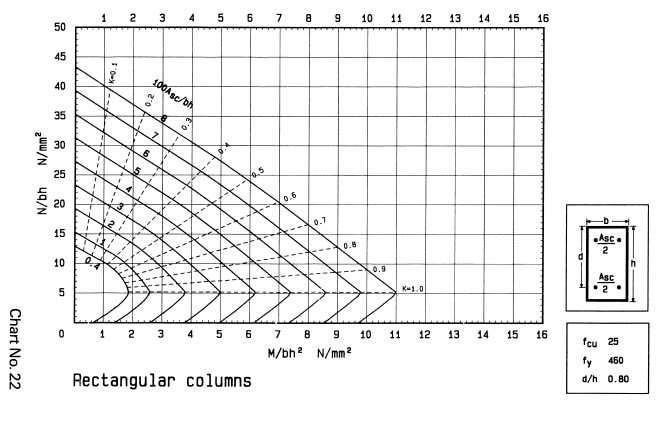
From the design chart, the intersection of M/bh² = 6.1 and N/bh = 39.6 falls outside the boundary of the curve. This means the load and moment acting on the column exceeds its capacity. To circumvent this, we shall increase the height of the column (h) to 350mm. By this the column cross-section becomes 250 x 350mm.

 

We re-determine the parameters

 

1. Determine N/bh

 

N/bh = 2478.55 x 10^3 /250 x 350    = 28.3

 

1. Determine M/bh²

M/bh² =    95.66 x 10^6/250 x 350² = 1.4

 

1. Calculate d/h

d/h determines the exact graph that shall be used to determine the reinforcement area.

d = h – c – d – d/2

= 350 -25 – 10 – 16/2 = 307

d/h   = 307/350 = 0.87

d/h is approximated to 0.9. This time around Chart No 24 is used. the intersection of M/bh² = 1.4 and N/bh = 28.3 falls on the 5.0 mark, this is shown with the red lines drawn on the chart as displayed below:

 

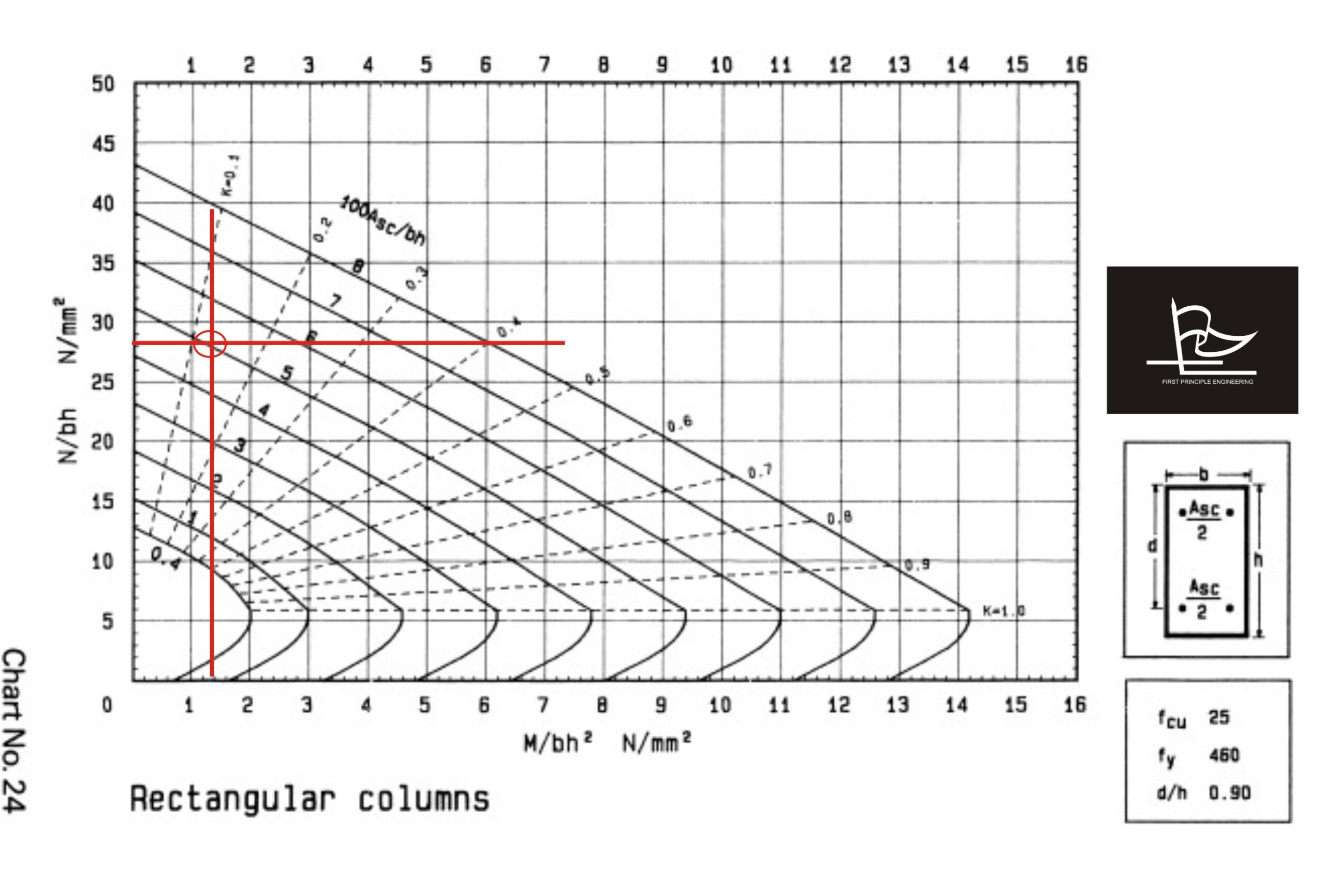
Hence from the design chart:

100A_sc/bh = 5.0

A_sc = 5.0 x 250 x 350/100

A_sc= 4375mm²

Provide 9Y25 (4393mm²) as longitudinal bars.

 

• Check minimum and maximum area of reinforcement requirement

From the design chart it is obvious the minimum and maximum area of reinforcement requirement are satisfied as the percentage area of reinforcement (100A_sc/bh) is higher than the lower boundary 0.4 and lower than the upper boundary 6.0

(Note: The 8.0 limit on the design chart is meant for horizontally cast columns which is not what we have in this example)

ie: 0.4 ≤ 100A_sc/bh ≤ 6.0

 

• Determine the link diameter and spacing

1. Link diameter

The link diameter is the greater of;

• ¼ x maximum diameter of longitudinal bar
• 6mm

¼ x maximum diameter of longitudinal bar = ¼ x 25 = 6.25mm

Hence use 10mm as the link diameter.

 

          2. Link Spacing

The link spacing should be;

• 12 x minimum diameter of longitudinal bar

12 x minimum diameter of longitudinal bar = 12 x 25 = 300mm

 Provide 10mm links at 250mm spacing.

 

Detailing

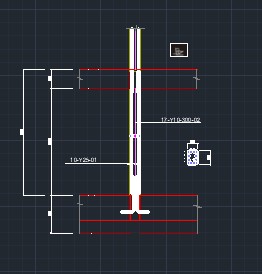
NB: For symmetry of the reinforcement, 10Y25 is provided rather than 9Y25 enumerated in the design.