INTRODUCTION
A structure is said to be in a state of static equilibrium if it is at rest. For a structure to be at rest, the forces acting on it must balance each other out along or about any axis so that the net force on the structure is zero.
Examples of this scenario abound us in our daily lives. A person sitting on a chair is at rest not because there are no forces acting on him but because the forces acting on him counterbalance each other. The gravitational force acting downward on him is canceled out by the upward reaction of the chair on his buttocks. If the chair is abruptly pulled away from under his buttocks thereby eliminating the counterbalancing reaction, the man will accelerate downward under the force of gravity until he hits the ground. He thereby remains at rest again as the ground surface exerts again a reaction force that once again counterbalances the gravitational force on him!
Equations of Static Equilibrium
There are mathematical expressions that must be satisfied before a structure can be in a static state. These equations are derived from Newton’s second law of motion: F = ma.
In a condition of static equilibrium, the acceleration of the structure is zero so the equation becomes:
F = 0
The above expression implies all forces acting on the structure must balance one another out such that the algebraic force on the structure is zero.
The equation is better modified as ∑ F = 0
In a three-dimensional structure or space frames such as the ones we model and analyze in various structural engineering software, three axes are always present, which are: Y axis, X axis, and Z axis. Along each axis, the equation F = 0 must be satisfied for the structure to be in a state of static equilibrium. This can me expressed mathematically thus:
Fx= 0
Fy = 0
Fz = 0
Furthermore, the moment taking about any point lying on any of the three axes must be zero. The structure must be stable against overturning. This brings about the equations:
Mx = 0
My = 0
Mz = 0
All these six equations put together are what is called the equations of static equilibrium.
What if our structure is a 2D element like a simple beam or a planar frame?
IF our structure is two-dimensional, forces will only act along two axis which are x and y, and there will be a single moment about Z axis. This represents the configuration of typical members such as beams, columns, and planar truss on which we run hand-based computations. Many three-dimensional structures are discretized into various two-dimensional structures or element for ease of computations. In such two-dimensional planar structures, there are only three equation of static equilibrium which are:
Fx = 0
Fy = 0
Mz = 0
Calculating forces acting on a member using static equilibrium Equation: Worked Example
Using the equations of static equilibrium, calculate the reactions on the beam below
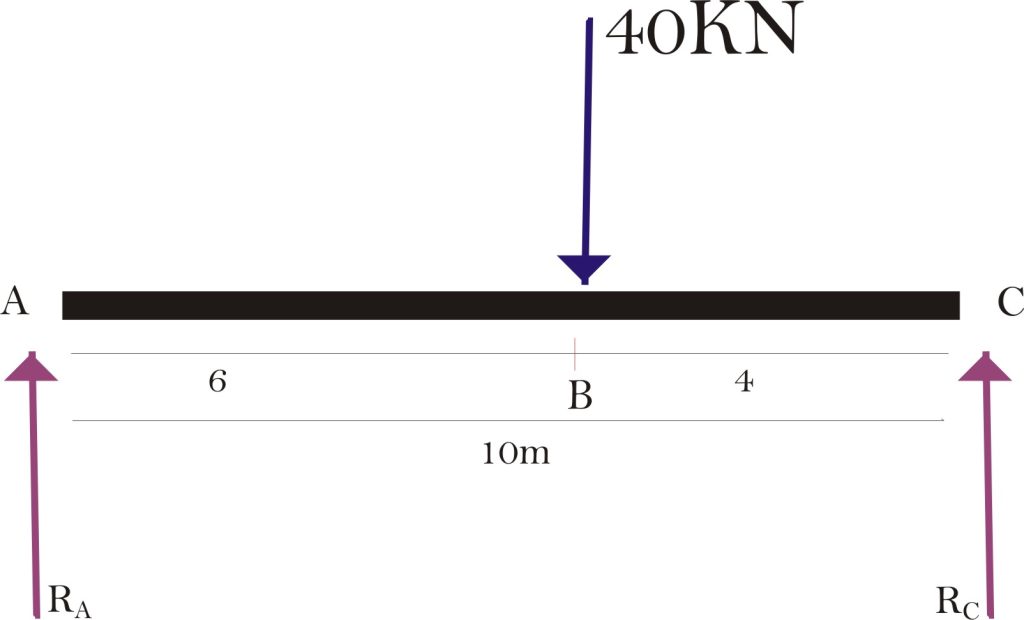
Taking moment about point C. The total moment about C must be equal to zero, taking clockwise moment as positive.
RA x 10 – 40 x 4 = 0
RA = 160/10
RA = 16KN
Summation of upward forces equals to zero, taking upward forces as positive.
RA + RC – 40 = 0
RC = 40 – RA
RC = 40 – 16
RC = 24KN
