1.0 INTRODUCTION
Before any structure can be designed, structural analysis must be performed to determine the effect of actions on the structure. However, before structural analysis can be successfully executed to solve for internal stresses and deformations, it is pertinent that the support condition of the structure is such that the structure is statically stable.
2.0 How do we know a structure is stable?
When using one of the numerous structural analysis software, the engineer needs not get himself worked up to determine whether the structure is stable due to its support conditions. The software will readily display error warnings to call the attention of the engineer to the inherent instability. It is left for the engineer to interpret the warning note and investigate the point of concern and then proffer necessary solution to ensure stability.
A structure is said to be stable if it assumes back the position of equilibrium after a disturbance or an excitation. This means enough reactions are summoned from the support(s) of the structure to resist actions on it without causing excessive deformation or outright displacement. To achieve this in the context of linear static analysis, one of the criteria is that the number of reactions acting on the structure must be at least equal to the number of equations of static equilibrium.
For a planar structure or element (i.e.: a 2D member like a beam), the total number of reactions must be at least three for stability. If the total number of reactions is less than three, then the structure is unstable and will collapse even under its own weight. Hence, a structure which has its number of reactions to be less than the number of equations of static equilibrium is said to be unstable.
2.1 Supports and Reaction Component
It has been learnt from the above paragraphs that to verify the stability of a structure due to support conditions the numbers of equation of static equilibrium have to be compared against the number of reactions acting on the structure. It is therefore necessary to be able to identify different types of supports and their corresponding reactions so that the stability of a structure can be correctly examined. Below are the types of supports and respective reactions.
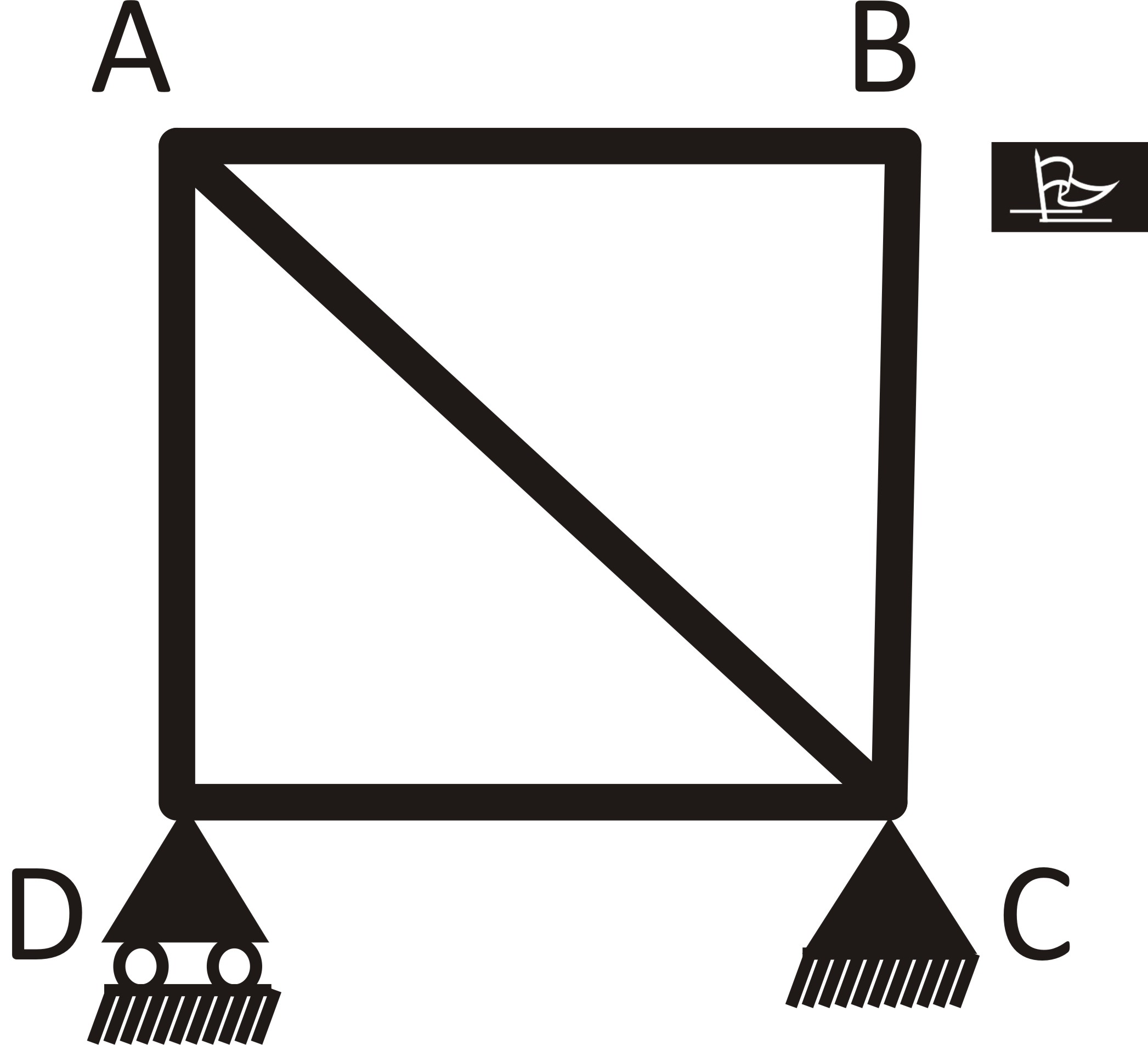
- Roller supports: A roller support provides one degree of restraint such that it resists displacement only in the vertical direction. The structure can displace horizontally or rotate.

fig (1) Roller support and its reaction component - Hinge/pinned Supports: A hinge support has two degrees of restraints such that it resists displacement in both vertical and horizontal direction. It however allows rotation.

fig (2) Hinge Support and its reaction components - Fixed supports: A fixed support provides three degrees of restraint as it does not allow translational displacement in both vertical and horizontal direction and neither does it allow rotation. This type of support is also called rigid support.

fig (3) Fixed Support and its reaction components 2.2 Worked Examples 1: Evaluating the support conditions of member on stability.
Determine whether the support reactions of the members below are enough to achieve stability.
1)

The beam has two roller supports. The reaction at each support is one which makes the total reactions on the beam to be 2.
Number of equilibrium equation = 3
Number of reactions = 2
Since Number of equations > Number of reactions, then the beam is unstable.
2)

The beam in example (2) has one roller support and one hinge support. The total reactions on the beam are three (one reaction from the roller support plus two reactions from the hinge support).
Number of equilibrium equation = 3
Number of reactions = 3
Since Number of equations = Number of reactions, then the structure is stable
3)

The beam in example (3) has one fixed support. The total reactions on the beam are three.
Number of equilibrium equation = 3
Number of reactions = 3
Since Number of equations = Number of reactions, then the beam is stable
2.3 Other Conditions for Stability
Besides the condition in the preceding paragraphs that the number of reactions on a structure must be at least equal to the number of equations of equilibrium, other conditions that has to be met are:
- The reactions must not be all parallel
- The reactions must not be all concurrent such that they all pass through a common point.
3.0 Determinacy and Indeterminacy
3.1 Determinate Structure
A determinate structure is a structure that can be analyzed using only the equations of static equilibrium. For a determinate structure, the support reactions and internal forces – such as shear forces and bending moments – can be computed using the equilibrium equations alone.
A planar structure is determinate if the number of reactions is equal to three which is the same as the number of equilibrium equations (Fx=0, Fy = 0, Mz= 0).
It can also be said that a structure is determinate when its degree of indeterminacy is zero. The degree of indeterminacy is equals to the number of surplus reaction(s) obtained after subtracting the number of equilibrium equations from the number of support reactions acting on the structure. The surplus reactions are also called redundant.
Examples of members that are determinate are simply supported beam, cantilever beam, etc.
3.2 Indeterminate Structure
An indeterminate structure is a structure that cannot be analyzed solely by using the equations of static equilibrium. The structure can only be analyzed by combining equilibrium equations and compatibility equations.
For a planar structure if the number of reactions acting on the structure is more than three then the structure is indeterminate.
It can also be said that a structure is indeterminate if its degree of indeterminacy is greater than zero.
Structures that fall under this are continuous beam, propped cantilever, etc.
3.3 Worked Examples 2: Evaluating the determinacy and degree of indeterminacy of members.
Determine whether the beams shown below are determinate or indeterminate, and if they are indeterminate, determine their degree of indeterminacy.
1)
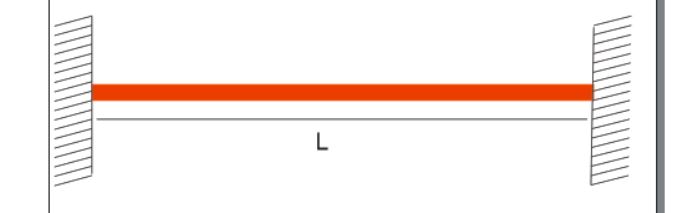
The beam is fixed at both ends.
A fixed ends has three reactions. Since both ends are fixed, the beam is subjected to six reactions
Determinacy Check:
6 reactions > 3 equilibrium equations
The beam is indeterminate.
Degree of indeterminacy:
The degree of indeterminacy is obtained by subtracting the number of reactions from the number of equilibrium equations.
6 – 3 = 3
The degree of indeterminacy of the beam is 3.
2)
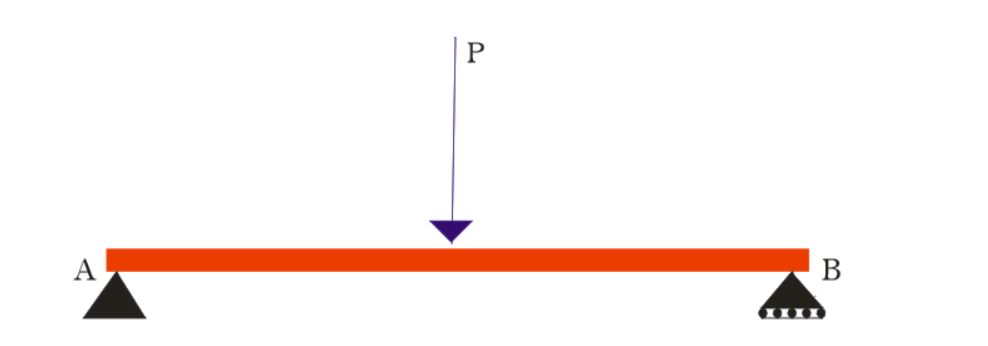
The beam has hinge support on the left end and roller support on the right end.
Hinge supports has two reactions
Roller support has one reaction
Total reactions on the beam = 3
Determinacy Check:
3 reactions = 3 equilibrium equations
The beam is determinate
Degree of indeterminacy:
The degree of indeterminacy is obtained by subtracting the number of reactions from the number of equilibrium equations.
3 – 3 = 0
The degree of indeterminacy of the beam is 0
3.4 Determinacy and Indeterminacy of a truss system
A truss system is an assemblage of members fastened together by pin to form a triangulated structure that is inherently stable.
The basic number of members in a truss is three (see fig(i)) so as to form a triangle. When there is need to extend the truss; two members, and one joint are added one at a time so that the new extension also forms another triangle thereby maintaining the structure’s internal stability (see fig(ii) and fig(iii)).

Since the basic number of members in a truss is three and additional two members per each subsequent joint can be added to extend the truss to as many members as desire, the total number of members in any given truss can be expressed as follows:
M = (No of basic members) + 2 x (No of subsequent joints)
M = 3 + 2 x (n– 3)
M = 3 + 2(n – 3)
M = 2n -3
Where: M = number of members in the truss
n = No of joints in the truss
NB: If a given truss has the number of its actual members to be greater than the result obtained from the formular: M = 2n – 3; then the surplus members are redundant members.
To get the overall determinacy or otherwise of a truss, the ideal number of members and number of equilibrium equations are added together thus:
Number of members + Number of equilibrium equations
M +r
Where: M = 2n-3.
r = 3
M + r = 2n – 3 + 3
M + r = 2n
2n is compared against the actual sum of the number of members in the truss, and numbers of actual reactions based on the type of supports. If the actual sum is greater than 2n, the truss is indeterminate, however if the actual sum equals to 2n, the truss is determinate.
3.4.1 Worked Examples 3: Evaluating the indeterminacy of trusses.
Determine whether the below trusses are determinate or indeterminate.
1)
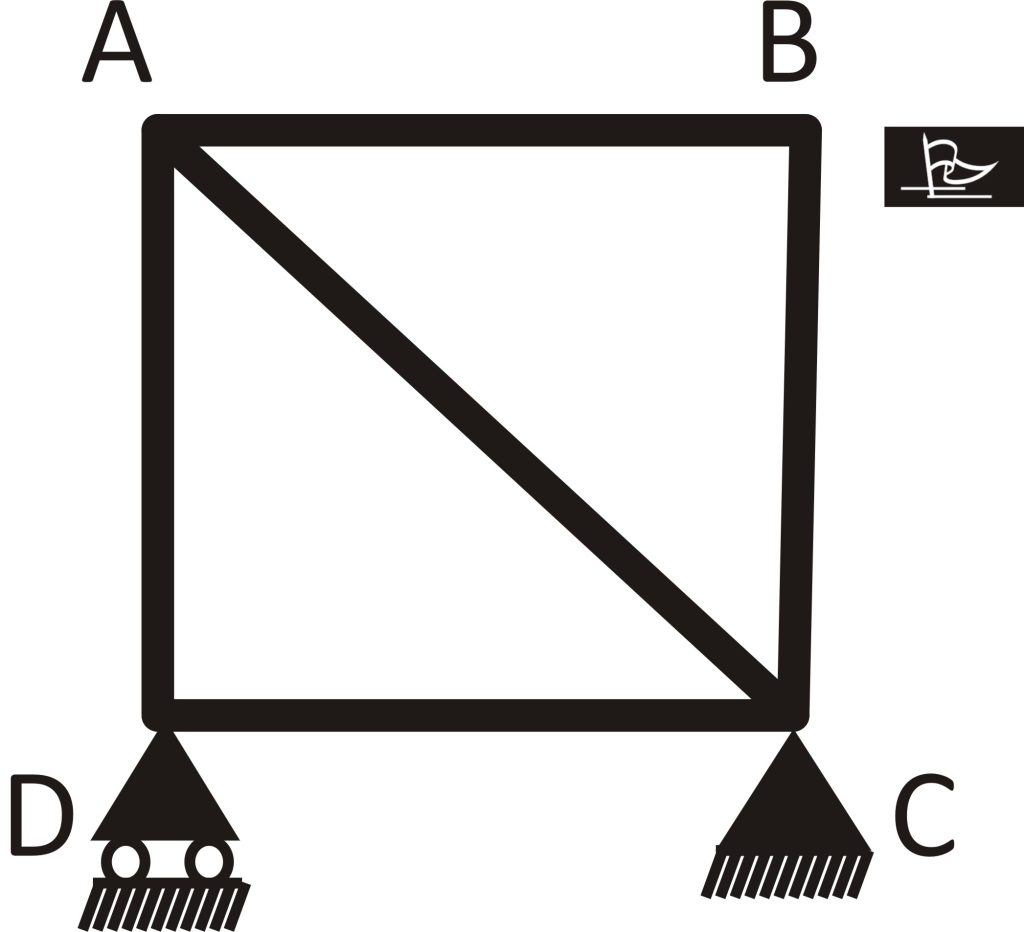
Using the formular
The number of joints in the truss is 4, using M + r = 2n
M + r = 2 x 4 = 8 … (1)
Inspecting the truss
On inspection the truss has 5 members and 3 reactions
M + r = 5 + 3 = 8 … (2)
Since (1) = (2), then the truss is determinate.
2)
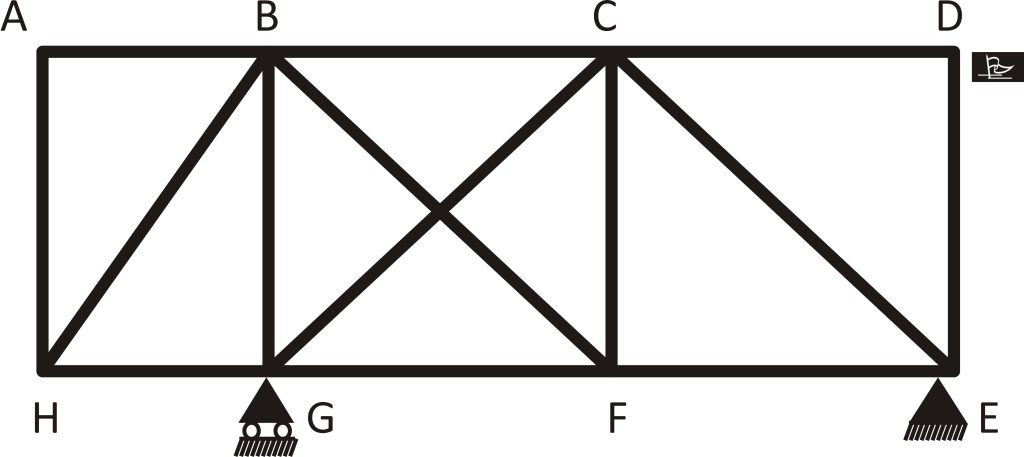
Using the formular
The number of joints in the truss is 8, using M + r = 2n
M + r = 2 x 8 = 16 … (1)
Inspecting the truss
On inspection the truss has 14 members and 3 reactions
M + r = 14 + 3 = 17 … (2)
Since (1) < (2), then the truss is indeterminate to one degree.



You are a very persuasive writer. I can see this in your article. You have a way of writing compelling information that sparks much interest.
For the reason that the admin of this site is working, no
uncertainty very rapidly it will be famous, due to its quality contents.
Your point of view caught my eye and was very interesting. Thanks. I have a question for you.
My spouse and I absolutely love your blog and find nearly all of your
post’s to be exactly what I’m looking for. Would you offer guest writers to write content for you?
I wouldn’t mind composing a post or elaborating on a number of the subjects you write related
to here. Again, awesome website!
Hi! I realize this is somewhat off-topic but I
needed to ask. Does running a well-established blog such as yours take a large amount of work?
I am brand new to blogging however I do write in my diary on a daily basis.
I’d like to start a blog so I can easily share my personal experience and thoughts online.
Please let me know if you have any kind of suggestions or tips for new aspiring blog owners.
Appreciate it!
Its like you read my thoughts! You seem to know so much about this,
such as you wrote the e book in it or something. I feel that you simply could do with a few p.c.
to power the message house a little bit, however other than that, this is fantastic blog.
A great read. I will certainly be back.
Fantastic beat ! I would like to apprentice while you amend your web site, how can i subscribe for a
blog website? The account aided me a acceptable deal.
I had been tiny bit acquainted of this your broadcast offered bright clear concept
It’s nearly impossible to find experienced people about this topic, but you seem like you
know what you’re talking about! Thanks
Thank you for the good writeup. It in fact
was a amusement account it. Look advanced to
more added agreeable from you! However, how could we communicate?
What’s Going down i’m new to this, I stumbled upon this I
have found It absolutely helpful and it has helped me out loads.
I hope to give a contribution & aid other customers like
its aided me. Good job.
Thanks for sharing. I read many of your blog posts, cool, your blog is very good.
Hi are using WordPress for your blog platform? I’m new to
the blog world but I’m trying to get started and
create my own. Do you need any coding knowledge to
make your own blog? Any help would be really appreciated!
Your point of view caught my eye and was very interesting. Thanks. I have a question for you.
hey there and thank you for your info – I have certainly picked up something
new from right here. I did however expertise several technical issues using this web
site, as I experienced to reload the web site many times previous to I could
get it to load correctly. I had been wondering if your web host
is OK? Not that I am complaining, but slow loading instances times will often affect your placement
in google and could damage your high quality score if ads and marketing
with Adwords. Well I’m adding this RSS to my e-mail and could look out for a lot
more of your respective intriguing content.
Make sure you update this again very soon.
You should be a part of a contest for one of the greatest
websites online. I am going to recommend this web site!
I know this if off topic but I’m looking into starting my own weblog and was wondering what all is needed to get set up?
I’m assuming having a blog like yours would cost a pretty penny?
I’m not very internet smart so I’m not 100% positive.
Any recommendations or advice would be greatly appreciated.
Appreciate it
Amazing! This blog looks exactly like my old one!
It’s on a entirely different subject but it has pretty much the same page layout and design. Wonderful choice of colors!
Fascinating blog! Is your theme custom made or
did you download it from somewhere? A theme like yours
with a few simple tweeks would really make my blog jump out.
Please let me know where you got your design. Thank you
Excellent, what a webpage it is! This weblog presents
helpful data to us, keep it up.
Hey! Do you know if they make any plugins to protect against hackers?
I’m kinda paranoid about losing everything I’ve worked hard on. Any tips?
Appreciate this post. Let me try it out.
Definitely believe that which you stated. Your favorite justification appeared to be on the web the simplest thing to be aware of.
I say to you, I definitely get annoyed while people consider worries that
they plainly do not know about. You managed to hit the nail
upon the top and also defined out the whole thing without having side effect , people could take a signal.
Will probably be back to get more. Thanks
Excellent site. Plenty of helpful info here.
I’m sending it to several pals ans also sharing in delicious.
And naturally, thanks in your effort!
Thank you for the auspicious writeup. It in fact used to be a
leisure account it. Glance advanced to far delivered agreeable from you!
By the way, how can we communicate?
Have you ever thought about including a little bit more than just your
articles? I mean, what you say is important and everything.
But think of if you added some great images or video clips
to give your posts more, “pop”! Your content is excellent but with images and video
clips, this site could undeniably be one of the greatest in its field.
Excellent blog!
Hello, just wanted to mention, I enjoyed this article.
It was practical. Keep on posting!
Do you have a spam problem on this site; I also am a blogger, and
I was wondering your situation; many of us have developed some nice procedures
and we are looking to trade techniques with others, please shoot me an e-mail if interested.
I was recommended this blog by my cousin. I’m not sure whether this post is written by him as nobody else know such detailed about my problem.
You are wonderful! Thanks!
Great article, exactly what I was looking for.
Today, I went to the beach front with my kids.
I found a sea shell and gave it to my 4 year old daughter and said “You can hear the ocean if you put this to your ear.”
She placed the shell to her ear and screamed. There was a hermit
crab inside and it pinched her ear. She never wants to go
back! LoL I know this is totally off topic but I had to tell someone!
It’s remarkable to pay a quick visit this web site and reading
the views of all colleagues concerning this piece of
writing, while I am also zealous of getting familiarity.
Excellent article. Keep posting such kind of info on your page.
Im really impressed by your blog.
Hi there, You’ve done an incredible job. I’ll certainly digg it and
personally suggest to my friends. I am sure they will be benefited from this site.
Howdy, i read your blog occasionally and i own a similar one and i
was just curious if you get a lot of spam feedback?
If so how do you protect against it, any plugin or anything you can advise?
I get so much lately it’s driving me mad so
any help is very much appreciated.
Hello there! This post could not be written any better!
Reading this post reminds me of my previous room mate!
He always kept talking about this. I will forward this page to him.
Pretty sure he will have a good read. Many thanks for
sharing!
Because the admin of this website is working, no question very quickly it will be renowned, due to its quality
contents.
Now I am going away to do my breakfast, afterward having my breakfast coming again to read
more news.
Yes! Finally someone writes about website.
Normally I do not learn post on blogs, however I would like to say that this write-up very forced me to check out and
do it! Your writing taste has been amazed me. Thanks, quite nice post.
Thanks for the marvelous posting! I quite enjoyed reading it,
you are a great author.I will make sure to bookmark
your blog and definitely will come back later in life.
I want to encourage you to ultimately continue your great writing, have a nice day!
Thanks for some other excellent article. The place else
may just anyone get that kind of info in such an ideal manner
of writing? I’ve a presentation next week, and I’m at the search for such information.
You should be a part of a contest for one of the finest sites on the
web. I’m going to recommend this site!
I have been exploring for a little for any high quality articles or blog posts
in this kind of area . Exploring in Yahoo I at last stumbled upon this site.
Reading this information So i’m happy to show that I have
a very just right uncanny feeling I came upon just what I
needed. I so much indisputably will make sure to don?t disregard this website and give it
a glance on a relentless basis.
you are truly a just right webmaster. The website loading speed
is amazing. It kind of feels that you are doing any
unique trick. In addition, The contents are masterwork.
you have done a excellent task in this subject!
Awesome! Its genuinely amazing piece of writing, I have got much clear idea on the
topic of from this piece of writing.
Hmm is anyone else having problems with the pictures on this blog loading?
I’m trying to figure out if its a problem on my end or if it’s the
blog. Any feedback would be greatly appreciated.
Post writing is also a excitement, if you know
after that you can write if not it is difficult to write.
Thank you for sharing your info. I really appreciate your efforts
and I am waiting for your further write ups thank you once again.
Heya i am for the first time here. I found this board and I find It truly useful & it helped me out
a lot. I hope to give something back and aid others like you aided me.
Howdy! Someone in my Facebook group shared this site with us
so I came to look it over. I’m definitely enjoying the information. I’m bookmarking and will
be tweeting this to my followers! Superb blog and terrific design.
Hey I know this is off topic but I was wondering if you knew of any widgets I could
add to my blog that automatically tweet my newest twitter updates.
I’ve been looking for a plug-in like this for quite some time and was
hoping maybe you would have some experience with something like this.
Please let me know if you run into anything.
I truly enjoy reading your blog and I look forward to your new updates.
I have read so many articles on the topic of the blogger lovers but this piece of writing is genuinely a fastidious article, keep it up.
I am extremely impressed with your writing skills and also with the layout on your blog.
Is this a paid theme or did you customize it yourself?
Either way keep up the nice quality writing, it’s rare to see a great blog like this one nowadays.
I am really impressed with your writing abilities as neatly as with
the structure on your weblog. Is that this a paid subject or did
you customize it your self? Either way keep up the nice quality writing, it is rare to peer a nice weblog like this one nowadays..
I know this if off topic but I’m looking into starting my own weblog and was wondering what all is required to get
setup? I’m assuming having a blog like yours would cost a pretty penny?
I’m not very web savvy so I’m not 100% positive. Any suggestions or advice would be greatly appreciated.
Thanks
I’m extremely impressed with your writing skills and also
with the layout on your weblog. Is this a paid theme or did
you customize it yourself? Anyway keep up the nice quality writing, it is rare to see a great blog like this one nowadays.
If you are going for most excellent contents like I do, simply pay a quick visit this web page
all the time since it gives quality contents, thanks
Informative article, just what I was looking for.
What’s up mates, fastidious post and good arguments commented at this place, I am truly enjoying
by these.
Having read this I thought it was rather enlightening.
I appreciate you finding the time and effort to put this information together.
I once again find myself spending a lot of time both
reading and leaving comments. But so what, it was still worth it!
Today, I went to the beachfront with my kids. I found a sea shell and
gave it to my 4 year old daughter and said “You can hear the ocean if you put this to your ear.” She put the
shell to her ear and screamed. There was a hermit crab inside and it pinched her ear.
She never wants to go back! LoL I know this is entirely
off topic but I had to tell someone!
время 23:32 значение, 22 32 на часах – значение дама бубен в
гадании, бубновая дама знак зодиака научиться карта
таро онлайн бесплатно к чему снится змея без головы, к
чему снится змея в воде проснуться от падения во
сне, падение во сне в исламе
I got what you mean , appreciate it for posting.Woh I am thankful to find this website through google.
Magnificent goods from you, man. I’ve be aware your stuff prior to and you are just too great. I really like what you have bought here, really like what you are stating and the way wherein you are saying it. You make it entertaining and you still care for to keep it sensible. I can’t wait to learn far more from you. This is actually a terrific web site.