A slender column is a column that is vulnerable to buckling which prevents it from harnessing its maximum strength. Several codes of practice have devised diverse methods to analyse this type of column with focus on stimulating its inherent instability by augmenting the moments from the general first-order analysis with additional moment. This will enable the column to be designed and sized appropriately for the most onerous case throughout its service life.

The Eurocode 2 also has several methods of analysing a slender column, however the method favored in this article shall be the nominal curvature method as discussed in clause 5.8.8 of the code. Hence, this article presents a worked example of design of slender column to Eurocode 2 using the nominal curvature method.  

Worked Example

The column that shall be designed is column BD that has already been analysed here for moment as part of a frame. Since the column has already been evaluated to be subjected to a moment of 42.302KNm, we are left to evaluate the axial force acting on the column.

The axial force of a column in a structural frame may be calculated on the assumption that beams and slabs transmitting force into the particular column are simply supported. By this, the reaction from the column can be calculated which in turn serves as the load on the column. The axial force on the column BD is calculated below.  

Computation of Axial load

            For easy computation of axial load, the analysed frame is reproduced below:  

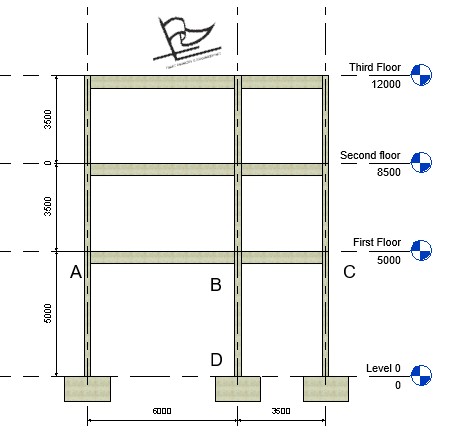
Since we are computing for the axial load, the maximum ultimate load is used all through as this gives the unfavorable axial load possible.

 

Third Floor Load take down

Characteristic permanent load on beam (gk) = 23KN/m

Characteristic variable load on beam (qk) = 36KN/m

Maximum ultimate Load acting on beam = 1.35(23) + 1.5(36) = 85KN/m  

 

Load from third floor to column BD = (6/2 + 3.5/2) X 85 = 403.75KN   

 

Second Floor and First Floor Load take down

Characteristic permanent load on beam (gk) = 100KN/m

Characteristic variable load on beam (qk) = 40KN/m

Maximum ultimate Load acting on beam = 1.35(40) + 1.5(100) = 195KN/m  

 

Load from second floor to column BD = (6/2 + 3.5/2) X 195 = 926.25KN

Load from first floor to column BD = (6/2 + 3.5/2) X 195 = 926.25KN    

 

Axial Load on Column BD Total Axial load on column BD = 403.75 + 926.25 + 926.25 = 2256.25KN  

 

Steps in designing the column

Having calculated the axial load on the column, we can now proceed with the design of the column. However, before embarking on the proper design, let us write down the loads and other design parameters necessary for the column design.

Moment on the column (M) = 42.302KNm

Axial load on the column (N) = 2256.25KN

Length (l) = 5m

Breadth (b) = 250mm

Height (h) = 250mm

fck = 25N/mm2

cover = 25mm  

  1.  Check the Slenderness of the column.

The slenderness ratio of the column shall be compared against the limiting slenderness, if the slenderness ratio is greater than the limiting slenderness then the column is declared “slender”. The column is declared “non-slender” if otherwise. This is shown in the below steps

a)  Calculate the effective length of the column

Since the column is braced, the Effective length (lo) is calculated thus:

$ _{\,\,l_0=0.5l\sqrt{\left( \text{1}+\,\,\frac{K_1}{\text{0.45}+\,\,K_1} \right) \left( \text{1}+\,\,\frac{K_2}{\text{0.45}+\,\,K_2} \right)}} $

K₁ and K₂ are the relative flexibilities of the top and bottom ends respectively

K₁=    $ \frac{\frac{\varSigma I_c}{l}}{\frac{\varSigma 2EI_b}{l}} $

$ \frac{\frac{\frac{bh^3}{12}}{l}}{2X\frac{\frac{bh^3}{12}}{l}\,\,+\,\,2X\frac{\frac{bh^3}{12}}{l}} $

$ \frac{\frac{\frac{250 X 250^3}{12}}{5000}}{2X\frac{\frac{225 X 500^3}{12}}{6000}\,\,+\,\,2X\frac{\frac{225 X 500^3}{12}}{3500}} $

= 65104.2/(781250 + 1339285.7)

= 0.031

 

We calculate K₂

The bottom end of column BD is assumed fixed in the subframe which implies the flexibility is 0. However, in accordance to Eurocode 2 guidance K2 is taken as 0.1 since fully rigid restraint is rare in actual practice (check 5.8.3.2 (3))

Hence;  K2= 0.1  

 

$ _{\,\,l_0=0.5l\sqrt{\left( \text{1}+\,\,\frac{0.031}{\text{0.45}+\,\,0.031} \right) \left( \text{1}+\,\,\frac{0.1}{\text{0.45}+\,\,0.1} \right)}} $ = 2803.2mm  

 

 b)  Calculate the radius of gyration

$ r\,\,=\,\,\sqrt{\frac{I}{A}}\,\,=\,\,\sqrt{\frac{\frac{bh^3}{12}}{b\,\,X\,\,h}}\,\,=\,\,\sqrt{\frac{\frac{\text{250}X\,\,250^3}{12}}{\text{250}X\,\,250}}\,\,\,\,=\,\,72.17 $  

 

c.  Calculate the slenderness ratio of the column

λ =    lo/r       = 2803.2mm/72.17      =     38.84  

 

d. Calculate the limiting slenderness

λ_lim = (20 X A X B X C/√n)

A = 0.7, B = 1.1, C = 0.7 (All these assumptions are based on alternative suggestion by the code, check clause 5:8:3:1)

n = N_Ed /A_cf_cd 

_{=    n = 2256.25 X 10^3 / (250 X 250 X  0.85 X 25/1.5) = 1.6}

λ_lim = (20 X 0.7 X 1.1 X 0.7/√1.6)  = 16.4

Since λ_lim (16.4) is less than ⅄ (38.84) then the column is slender and second-order moment is required.  

 

2.   Calculate the second-order moment

  Since the column is slender, second-order moment due to slenderness is necessary. Second-order moment (M₂ ) = N_ED +  e₂

where: N_ED is the design axial force.

e₂ is the deflection of the column  

Calculate deflection due to slenderness

e₂= 1/r l_o² / c

c = 10 (see 5:8:8:2 (4) of EC2)

e₂= 1/r x  2803.2²/ 10  

1. Calculate the curvature (1/r)

 1/r = Kr Ko 1/r_o  

Axial load correction factor (Kr)

K_r = (nu – n)/ (nu -n_bal) ≤ 1

nu = 1 + ω

ω = A_sf_yd/A_cf_cd

Assume As to be 4y16 = 799.7mm2

f_yd = 500/1.15 = 434.8

f_cd = 0.85 x 25/1.5 = 14.17

ω = (799.7 x 434.8)/ (250 x 250 x 14.17) = 0.393

nu = 1+ 0.393 = 1.393

nbal = 0.4  

n = Ned/Ac x fcd    =  2256.25/ (250 x 250 x 0.85 x 25/1.5 ) = 0.003

K_r = (1.393 – 0.003)/ (1.393 -0.4) = 1.4

Since 1.4 > 1, then Kr is taken as 1  

 

Creep Factor (Kϴ)

Kϴ = 1+ B ϕ_ef ≥ 1

B = 0.35 + fck/200 – ⅄/150

= 0.35 + 25/200 – 38.84/150 = 0.216

 effective creep ratio (ϕ_ef) = 2.14  (This conservative value is gotten by making ϕef the subject of formular in Equ 5.13N of Eurocode 2, when A is assumed to be 0.7)

Kϴ = 1+ 0.216 x 2.14 = 1.462

 

Calculate 1/r_o

1/r_o = fyd/(Es x 0.45d)

           434.8/ (200×10^3 x 0.45 x 250) = 0.00002

 

curvature (1/r) = 1 x 1.462 x 0.0002 = 0.00003

deflection due to slenderness (e₂) = 0.00003 x 2803.2^2 x 10 = 26.69mm

 

M₂ = 2256.25 x 26.69/1000 = 60.2KNm

 

3.  Compute the design moment (M_Ed)

The design moment is the greatest of:

 

1. max (M_o2, M_o1) + (N_ED) x max (e)

      2 M_oe+ M₂

      3. M_o1+ M₂/2

 

      Where:

M_o2 = 42.302KN

M_o1 = 0

M_oe= 0.4 M02 + 0.6 M01 = 16.9KNm

M₂ = 60.2KNm

 

1. max (M_o2, M_o1) + (N_ED) x max (e)

        = 42.302 + 2256.25 x 20/1000 = 87.427KNM

 

       2. M_oe+ M₂ = 16.9 + 60.2 = 77.13KNm

 

       3. M1+ M₂/2 = 0 + 60.2/2 = 30.1KNM

      The design moment is 87.427KNm

 

 4.  Use the design Chart to determine the area of reinforcement required

 In order to use the design chart, few parameters have to be calculated

Determine N_ED/bhfck

 

N_ED/bhfck = 2256.25X 10^3 /250 X 250 X 25   = 1.44

 

Determine M_ED/bh²fck

 

M_ED/bh²fck =    87.427 X 10^6/250 X 250^2 X 25   = 0.22

 

Calculate d’/h

d’/h determines the exact graph that shall be used to determine the reinforcement area.

d’ = c + d/2 = 25 + 16/2 = 33

            d’/h   = 33/250 = 0.13

This is approximated to 0.1 and the design chart peculiar to d’/h = 0.1 is used. Fig 9b of “How to design concrete Structures to Eurocode 2” matches this. The chart is reproduced below.

 

From the design chart, the intersection of M_ED/bh²fck = 0.22 and N_ED/bhfck = 1.44 is outside the boundary of the curve. The curve does not even have the value of 1.44 2hich corresponds to N/bhfck as it ends at 1.3. This means the load and moment acting on the column exceeds its capacity. To circumvent this, we shall increase the height of the column (h) to 350mm. By this the column cross-section becomes 250 x 350mm

 

We re-determine the parameters

1. Determine N_ED/bhfck

          N_ED/bhfck = 2256.25 x 10^3 /250 x 350 x 25   = 1.0

 

       2.  Determine M_Ed/bh2fck

M_Ed/bh2fck =    87.427 x 10^6/250 x 350^2 x 25   = 0.11

       3.  Calculate d’/h

d’/h determines the exact graph that shall be used to determine the reinforcement area.

d’ = c + d/2 = 25 + 16/2

      = 33

d’/h   = 33/350 = 0.09

 

d’/h is approximated to 0.1 and the same design chart is used.

 

M_Ed/bh²fck = 0.11 and N_ED/bhfck = 1.0 intersects at at 0.8 on the design chart. This is shown by the red mark drawn otn the design chart as displayed below.

Hence from the design chart:

 

A_sf_yk/bhf_ck   = 0.8

 

A_s = 0.8 x bhf_ck /f_yk

 

A_s = 0.8 x 250 x 350 x 25/ 500

 

A_s = 3500mm2

 

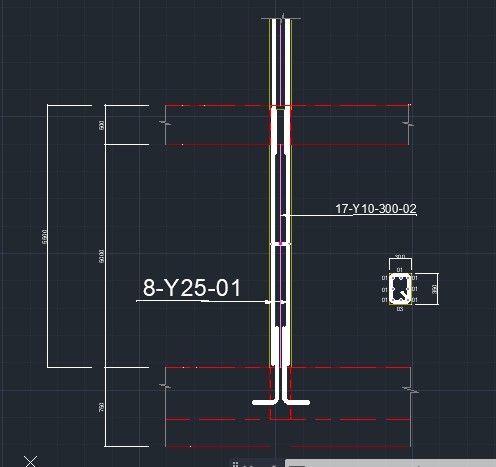
Provide 8Y25 (3905mm2) as longitudinal bars.

 

  5.  Check minimum required reinforcement

 

A_smin = 0.1Ned/fyd ≥ 0.002Ac

            = 518.93mm2

Since A_smin (518.93mm2) < As (3905mm2), minimum area of reinforcement is satisfied.

 

 6.  Check maximum area reinforcement

 

A_smax= 0.4 Ac = 0.4 x 250 x 350 = 3500mm2

 

Since A_s (3905mm2) is greater than A_smax (3500), we will increase the dimension of the column to satisfy maximum area requirement. We will increase the breadth (b) of the column to 300mm so that the column cross-section becomes 300 x 350mm.

 

Recheck maximum area of reinforcement

 

A_smax = 0.4 Ac = 0.4 x 300 x 350 = 4200mm2

 

Since A_s (3905mm2) is less than A_smax (4200mm2), maximum area of reinforcement requirement is now satisfied.

 

 7.  Determine the link diameter and spacing

 

      1. Link diameter

 

The link diameter is the greater of;

 

• ¼ x maximum diameter of longitudinal bar
• 6mm

 

¼ x maximum diameter of longitudinal bar = ¼ x 25 = 6.25mm

            Hence use 10mm as the link diameter.

 

     2.  Link Spacing

 

The link spacing should be the least of;

 

• 20 x minimum diameter of longitudinal bar
• lesser of the column dimension
• 400mm

 

• 20 x minimum diameter of longitudinal bar = 20 x 25 = 500mm

           lesser of the column dimension = 300m

            Since 300mm is lesser than 500mm and 400mm, 300mm governs the spacing

             Provide 10mm links at 300mm spacing.

 

Detailing