Design of a Doubly Reinforced Beam to BS 8110 – Worked example

This article presents a worked example on the design of doubly reinforced concrete beam to BS 8110

The image below shows the Plan view of a reinforced concrete structure, use the data given below to design Beam 2

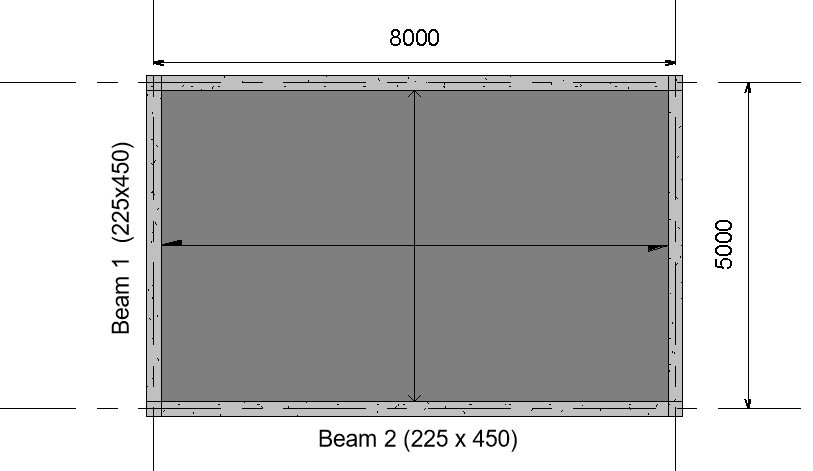
Design Data:

Variable load on slab =   5KN/m²

Finishes  =   1.5KN/m²

Unit weight of concrete   =   24KN/m³

Compressive strength of concrete (fcu)   =   25N/mm²

Characteristic Strength of main reinforcement (fy)  =  460N/mm²

Characteristic Strength of Shear reinforcement (fyv) =  460N/mm²

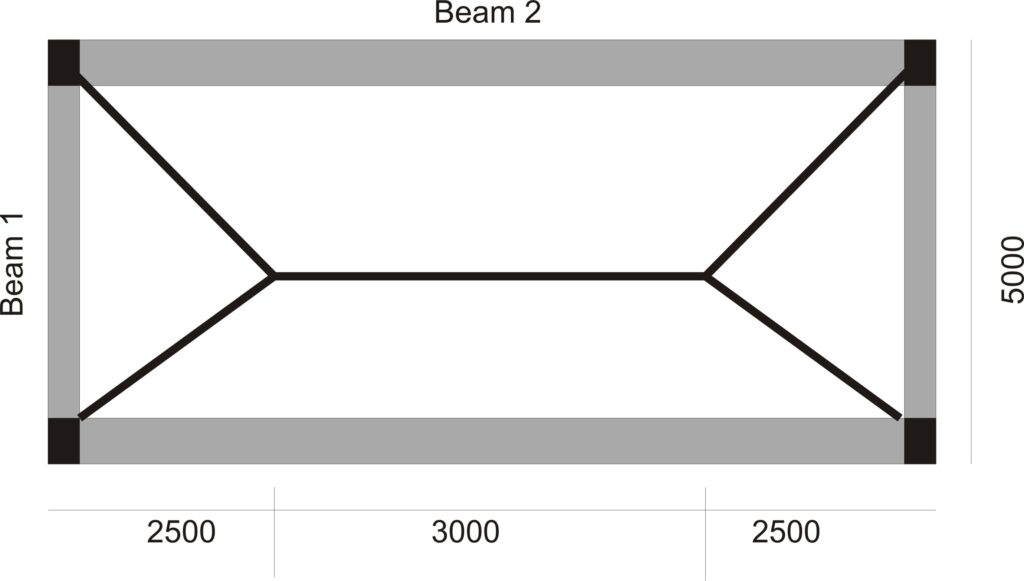
To design Beam 2, we will first distribute the slab loads on the beam and then analyze the beam to compute its internal forces. As shown in fig (2) below the tributary area of slab loads on beam 2 is a trapezium, hence we compute and distribute the slap loads on it as follows:

However, to understand the process of distributing slab load to beams in detail, read, “Distribution of Slab loads to beams.”

Analysis

Permanent Load

Characteristic Self-weight of slab = 0.2 x 24 = 4.8KN/m²

Partition Load on Slab = 1.5KN/m²

Characteristic Permanent Load on Slab   = 4.8 + 1.5 = 6.38KN/m²

Area of Slab load Supported by Beam 2   = (0.5 x (8 + 3) x 2.5)/8 = 1.73m²

Permanent Load of Slab on Beam 2 = 1.72 x 6.38 = 10.97KN/m

Self-weight of beam = 0.23 x 0.45 x 24    = 2.48KN/m

Total Permanent Load on beam = 10.97 +2.48 = 13.5 KN/m

Variable Load    

Variable load on slab = 5KN/m²

Area of Slab load Supported by Beam 2   = (0.5 x (8 + 3) x 2.5)/8   =   1.73m²

Characteristic Variable Load of Slab on Beam 2    = 1.258 x 5   = 8.59KN/m

Total Design Load

Ultimate Load acting on beam 2 = 1.4(13.5) + 1.6(8.59) = 32.3KN/m

Computation of Internal Forces:

The beam is assumed to be simply supported for ease of analysis.

M = w x L²/8 =   32.3 x 8²/8 = 258.5KNm

V   = W x L/2 =    32.3 x 8/2   = 129.24KN

Design

flexural strength design

1. Calculate the effective depth

Assume 25mm diameter for cover

Assume main reinforcement to be 16mm

Shear reinforcement to be 10mm

Effective depth = h-c-link diameter-o/2

                                = 450-25-10-8

                                = 407mm

2) Check whether section is to be designed as singly or doubly reinforced beam

$
K\,=\,\,\frac{M}{bd^2f_{cu}}
$

$
K\,=\,\,\frac{258.5×10^6}{225×450^2×25}
$

= 0.3

Since K (0.3) > K’ (0.156); design as doubly reinforced.

3) Calculate the lever arm (Z)

$
Z\,\,=\,\,d\left( 0.5+\sqrt{\text{0.25}-\,\,\frac{K’}{0.9}} \right)
$

$
Z\,\,=\,\,407\left( 0.5+\sqrt{\text{0.25}-\,\,\frac{0.3}{0.9}} \right)
$

Since 333.4 < 0.95d (386.7): use Z = 316

4. Calculate the area of compression steel required.

$
As’\,\,=\,\,\frac{M\,\,-\,\,0.156fcubd^2}{0.87f_y\left( d\,\,-\,\,d’ \right)}
$

$
As’\,\,=\,\,\frac{258.5×10^6\,\,-\,\,0.156 x 25 x 225 x 407^2}{0.87 x 460\left( 407\,\,-\,\,43 \right)}
$

As’ = 711mm²

Provide 4Y16 (799.7mm²)

5. Calculate the area of tensile steel

$
As\,\,=\,\,\frac{K’fcubd^2}{0.87f_yZ}\,\,+\,\,Asc
$

$
As\,\,=\,\,\frac{0.156 x 25 x 225 x 407^2}{0.87 x 460 x 316}\,\,+\,\,799
$

As = 1859mm²

Provide 11Y16 (2199mm²)

NB: You will observe that the area of tension reinforcement is large, this can be attributed to the 8m long span of the beam, and more overriding, the assumption that the beam is simply supported which then result in large span moment.

Shear Strength Design

1. Calculate the Shear Stress
   • v = V/bd
     • $\frac{129.24×10^3}{225×407}\,\,\,\,$
       • = 1.4N/mm²
2. Check whether the concrete section can resist the shear force without shear reinforcement.

$
v_{c\,\,=}\,\,\text{0.79}\left( \frac{100As}{b_vd} \right) ^{\text{1/}3}\frac{\left( \frac{400}{d} \right) ^{\text{1/}4}}{\gamma _m}
$

$
v_{c\,\,=}\,\,\text{0.79}\left( \frac{100 x 1859}{225 x 407} \right) ^{\text{1/}3}\frac{\left( \frac{400}{407} \right) ^{\text{1/}4}}{1.5}
$

v_c = 0.79N/mm²

Since  v_c(0.79)   < v (1.4); Shear reinforcement is required.

3. Check the form of shear links to be provided according to table 3.7.

0.5v_c =   0.5 x 0.79    = 0.4N/mm²

v_c + 0.4 =  0.79 + 0.4  = 1.2 N/mm²

Since  v > v_c+0.4; shear links must be designed and the shear stress (v) must be checked not to be more than 0.8xfcu^0.5  or 5N/mm²

0.8xfcu^0.5  =     0.8 x 25^0.5      =             4.0N/mm²         

Since v (1.4) is less than 0.8xfcu^0.5 (4.0) then the beam section is adequate and shear reinforcement only needs to be designed.

4. Calculate the required minimum shear links.

Assume two-legged shear reinforcement of 10mm is to be used.

Area of 10mm shear reinforcement = 78.58mm2

Area of two-legged 10mm links = 2x 78.58   = 157mm2

$
Asv_{}=\,\,\frac{b_v\,\,x\,\,s_v\left( v-v_c \right)}{0.95fy_v}\,\,
$

$
Asv_{}=\,\,\frac{225\,\,x\,\,s_v\left( 1.4-0.79 \right)}{0.95 x 460}\,\,
$

Substituting 157mm² for Asv and making sv the subject of the formular

s_v = 497mm

5) Check whether maximum spacing limit is satisfied

Smax = 0.75xd

= 0.75 x 407

= 305mm

Since 497mm is greater than maximum spacing limit, maximum spacing limit governs the design.

Hence: provide Y10 @ 300mm spacing.

Deflection Check

Deflection Check

1. Calculate the actual span-effective depth ratio

Span/depth ratio = 8000/407   = 19.7

2. Calculate the limiting Span-effective depth ratio

From table 3.9 of BS 8110, the basic Span/depth ratio for a simply supported beam is 20.

Tension reinforcement modification factor

$
\text{0.55}+\frac{477-\,\,f_s}{120\left( \text{0.9\,\,}+\,\,\frac{M}{bd^2} \right)}
$

where:

$
f_s\,\,=\,\,\frac{2f_yA_{sreq}}{3A_{sprov}}
$

$
f_s\,\,=\,\,\frac{2 x 460 x 1859}{3 x 2199 }
$

fs = 259.3

Substitute fs and values of other parameters into the tension modification formular

$
\text{0.55}+\frac{477-\,\,259.3}{120\left( \text{0.9\,\,}+\,\,\frac{258.5×10^6}{225 x 407^2} \right)}
$

= 0.78

Compression reinforcement modification factor

$
\frac{1+\frac{100Asprov}{bd}}{3+\frac{100Asprov}{bd}}
$

$
\frac{1+\frac{100 x 2199}{225 x 407}}{3+\frac{100 x 2199}{225 x 407}}
$

= 1.22

Modified basic span-effective depth ratio = basic span-effective depth ratio x M.F tension rebars x M.f compression rebars

Modified basic span-effective depth ratio = 20 x 0.78 x 1.22

= 19.15

Since Actual L/d (19.6) > modified Basic L/d (19.15); the beam fails deflection check.